Discrete control delay identification

This product note explains how to compute the discrete control delay of a control algorithm running on an imperix controller.

Context

The execution of a digital control algorithm inevitably introduces a delay along the control chain, which has an impact on the system response, and therefore on the achievable closed-loop control bandwidth.

This delay is key in the computation of controller parameters, such as \(K_p\) and \(K_i\) in the case of a PI controller. This note presents the different delays involved in the total loop delay and gives numerical examples of controller tuning.

Definitions of the various delays

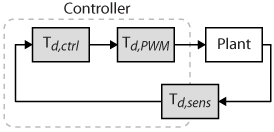
The total loop delay is the sum of all the delays involved between the measurement of a state variable and the resulting action of the controller on the controlled plant. The different delays involved are defined below.

Delay	Symbol	Definition
Sensing delay	\(T_{d,sens}\)	Delay in the measured quantity, due to finite sensor and analog chain bandwidth, and possibly filtering delay
Control delay	\(T_{d,ctrl}\)	Delay between sampling instant and duty-cycle update instant in the PWM modulator (FPGA peripheral)
Modulator delay	\(T_{d,PWM}\)	Average delay between duty-cycle update in the PWM modulator and resulting change in modulator output (see dedicated section below)
Switching delay	\(T_{d,tran}\)	Delay between change in the modulator output to actual switching of the power device (can often be neglected)
Total loop delay	\(T_{d,tot}\)	Sum of the above delays, representing the total delay of the control system

The control delay \(T_{d,ctrl}\) can be further divided into the following components (more information can be found in Timing info tab).

Delay	Symbol	Definition
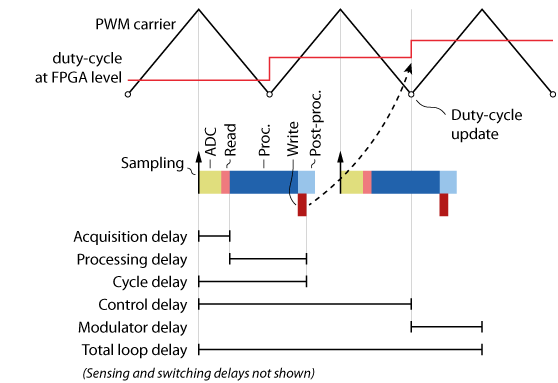
Acquisition delay	\(T_{acq}\)	Delay between sampling and data availability in CPU. = ADC conversion time (ADC in figure below) + FPGA-to-CPU transfer time (Read)
Processing delay	\(T_{pr}\)	CPU processing time (Proc.)
Write delay	\(T_{wr}\)	CPU-to-FPGA transfer time (Write)
Cycle delay	\(T_{cy}\)	Delay between sampling instant and newly computed data available in FPGA (\(T_{cy}=T_{acq}+T_{pr}+T_{wr}\), see dedicated section below)

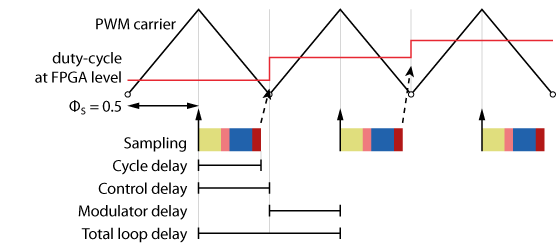
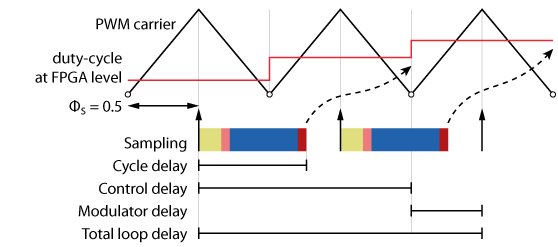
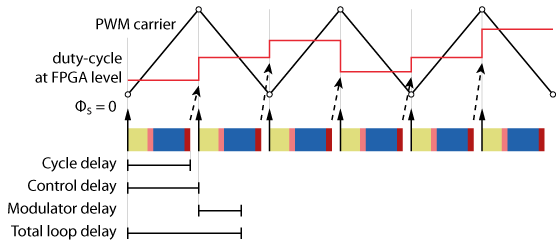
The figure below illustrates the different delays involved with a triangular PWM carrier and single-rate update of the duty-cycle (at the bottom of the carrier). 

Cycle delay

The cycle delay comprises the acquisition, processing, and FPGA transfer delays. Its value is computed inside the FPGA and displayed in the Target Info pane of imperix Cockpit.

Its value depends mainly on the complexity of the executed control algorithm and is thus application-dependent. For example, the control of the PV boost and three-phase grid-tied inverter (AN006) gives the following figures:

• Acquisition delay \(T_{acq}\): 2.072 µs (includes 2 µs ADC delay in B-Box RCP)
• Processing delay \(T_{pr}\): 3.9 µs
• Write delay \(T_{wr}\): 0.1 µs
• Cycle delay (total) \(T_{cy}\): 6 µs

Modulator delay

Most of the delays defined previously have pretty obvious definitions and are hardware-dependent. The modulator delay, however, merits further clarifications, since it takes several different values, depending on the PWM peripheral parameters. In all cases, the modulator delay represents the delay between the instant a new duty-cycle is taken into account in the PWM modulator, and the instant that new duty-cycle is reflected into a PWM pulse.

Sawtooth carrier

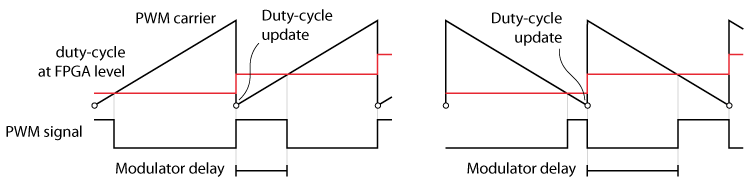
It is quite straightforward that the sawtooth carrier introduces a delay that depends on the duty-cycle \(d\) and the switching period \(T_{sw}\). From the figure below, we can deduce that the delay is

• Sawtooth carrier: \(T_{d,\text{PWM}}=dT_{sw}\)
• Inverted sawtooth carrier: \(T_{d,\text{PWM}}=(1-d)T_{sw}\)

For controller tuning, the average value \(T_{d,\text{PWM}}=0.5T_{sw}\) is generally used, for both sawtooth carrier shapes.

Triangular carrier

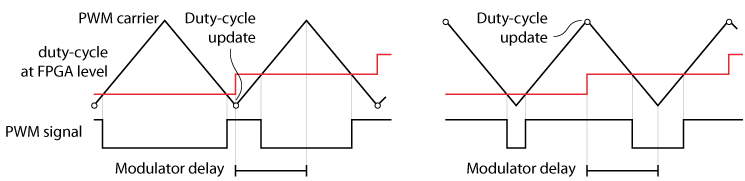
The modulator delay calculation is more tricky with a triangular carrier, since both rising and falling edges of the PWM signal are affected by the duty-cycle value.

A small-signal approximation introduced in [1] and further developed in [2] shows that \(T_{d,\text{PWM}}=T_{sw}/2\) for single-rate update.

Intuitively, the duty-cycle update has an effect on two PWM edges: before and after the half of the carrier, resulting, on average, in an effect after half a switching period [1]. This also means that the delay is identical for triangular and inverted triangular carriers.

With double-rate update, the modulator delay is reduced to \(T_{d,\text{PWM}}=T_{sw}/4\) [1], providing that the sampling is also performed at double rate (double-rate sampling, \(T_s=T_{sw}/2\)).

Direct output PWM

If no PWM modulator is used (e.g. when using the DO-PWM – Direct output PWM peripheral), the modulator delay is obviously \(T_{d,\text{PWM}}=0\). In this case, the firing signal is updated as soon as a new value is available at the FPGA level, meaning that \(T_{d,ctrl}=T_{cy}\).

Examples of delay calculation

Single-rate update

Let us consider the following standard configuration:

• The switching and sampling periods are the same \(T_{sw}=T_{s}\).
• The sampling phase is \(\phi_{s}=0.5\) to ensure sampling in the middle of the current ripples.
• The PWM modulator uses a triangular carrier with a phase of zero and single-rate update (i.e. update at the bottom of the carrier).
• The current sensor bandwidth is 200 kHz.

Regular control algorithm

In this first case, we assume that the control algorithm can be executed fast enough, so that the cycle delay is shorter than half a control period (\(T_{cy} < 0.5T_s\)). This is the case for most control implementations running on imperix controllers.

In this case, the total loop delay is computed as follows:

• Sensing delay: neglected (\(\approx 800\,\text{ns}\))
• Control delay: \(T_{d,ctrl} = 0.5T_s\)
• Modulator delay: \(T_{d,\text{PWM}}=T_{sw}/2\) (triangular carrier)
• Switching delay: neglected, sub-microsecond
• Total loop delay: \(T_{d,tot}=T_{d,ctrl}+T_{d,\text{PWM}}=T_s\)

Heavy control algorithm

Now let’s assume that the control algorithm is heavy and the cycle delay is longer than half a control period (\(T_{cy} \geq 0.5T_s\)).

In this case, the total loop delay is computed as follows:

• Sensing delay: neglected (\(\approx 800\,\text{ns}\))
• Control delay: \(T_{d,ctrl} = 1.5T_s\)
• Modulator delay: \(T_{d,\text{PWM}}=T_{sw}/2\) (triangular carrier)
• Switching delay: neglected, sub-microsecond
• Total loop delay: \(T_{d,tot}=T_{d,ctrl}+T_{d,\text{PWM}}=2T_s\)

General case

With single-rate update and triangular carrier, the total loop delay can take two values:

• If \(T_{cy} < (1-\phi_s)T_s\), \(T_{d,ctrl} = (1-\phi_s)T_s\) and \(T_{d,tot}=(1.5-\phi_s)T_s \)
• If \(T_{cy} \geq (1-\phi_s)T_s\), \(T_{d,ctrl} = (2-\phi_s)T_s\) and \(T_{d,tot}=(2.5-\phi_s)T_s\)

These results suggest that the smaller the sampling phase, the smaller the delay. However, the choice of the sampling phase should also rely on current ripple sampling considerations. Generally speaking, the choice of the sampling phase is a trade-off between control bandwidth and the accuracy of the control.

Double-rate update

Now let us consider the following configuration:

• The switching and sampling periods are \(T_{sw}=2T_{s}\) (double-rate sampling).
• The sampling phase is \(\phi_{s}=0\).
• The PWM modulator uses a triangular carrier with a phase of zero and double-rate update (update at the top and bottom of the carrier).
• The current sensor bandwidth is 200 kHz.

In this case, the total loop delay does not depend on the execution time of the algorithm, unlike with single-rate update. It is computed as follows:

• Sensing delay: neglected
• Control delay: \(T_{d,ctrl}=T_s\)
• Modulator delay: \(T_{d,\text{PWM}}=T_{sw}/4=T_s/2\) (triangular carrier with double-rate update)
• Switching delay: neglected, sub-microsecond
• Total loop delay: \(T_{d,tot}=T_{d,ctrl}+T_{d,\text{PWM}}=1.5T_s\)

References

[1] D. M. Van de Sype, K. De Gusseme, A. P. Van den Bossche and J. A. Melkebeek, “Small-signal Laplace-domain analysis of uniformly-sampled pulse-width modulators,” 2004 IEEE 35th Annual Power Electronics Specialists Conference, Aachen, Germany, 2004, pp. 4292-4298 Vol.6.

[2] S. Buso and P. Mattavelli, “Digital Control in Power Electronics”, 2006.