Discrete PI controller implementation

Table of Contents

This technical note addresses possible implementations for a discrete PI controller and provides general insight into PI tuning strategies. It also includes practical implementations for digital control, on Simulink, PLECS and C/C++.

General principles

PI controllers certainly represent the most intuitive and widespread form of closed-loop (feedback) control. As such, they are frequently implemented in both continuous (analog) and discrete (digital) domains. This is notably due to their simple structure and implementation, relying on two steps:

The difference between the desired setpoint and the measured variable is computed. This value is considered as an error.
The PI controller computes a control action that is proportional to this error (proportional part) and makes sure that the process output agrees with the setpoint in steady state (integral part).

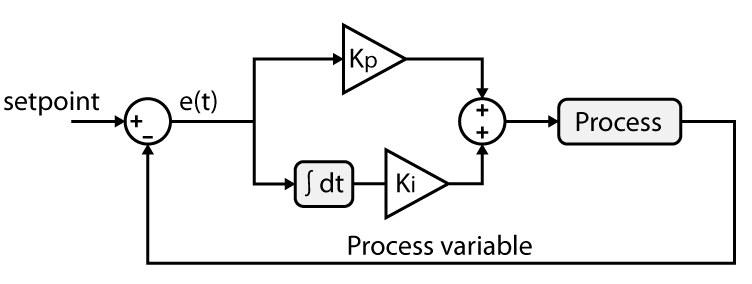
PI controller structure

Controller type

Imperix generally uses PI controllers and not PID controllers to avoid complexity and instability issues related to the derivative action. More precisely, the high-frequency gain of the derivative action can indeed cause amplification of measurement noise, which is undesirable. Also, PID controllers generally bring only little improvement when paired with first-order systems (which are very common in power electronics) [1].

Controller structure

PI controllers can be implemented either in parallel (also referred to as non-interacting), series (interacting), or mixed form [2]. This article, will focus on the parallel structure of PI controllers as it allows for the full decoupling of the proportional and integral term which makes manual tuning easier. The block diagram below describes the implementation of a parallel PI controller.

PI controller implementation, parallel form

Digital implementation

The well-known continuous time transfer function of a PI controller, given below, should be discretized to be implemented in a digital controller.

$$ (1) \quad C(s) = k_p + \frac{k_i}{s}$$

Here, $k_p$ and $k_i$ are the proportional and integral gain of the controller, respectively.

Usually, the main goals when discretizing a continuous function for a control system are to preserve its frequency behavior and stability characteristics. To this end, several possible discretization strategies exist, amongst which the three most common are Forward Euler, Backward Euler, and Tustin [3]. Each method comes with its advantages and drawbacks, which can be summarized as follows in order to guide the choice of implementation [4]:

Forward Euler: Simple and computationally efficient, but suffers from poor stability.
$$ (2) \quad s = \frac{z-1}{T_s} $$
Backward Euler: Unconditionally stable, but more computationally intensive than Forward Euler.
$$ (3) \quad s = \frac{z-1}{T_sz} $$
Tustin: Preserves continuous-time stability and offers superior frequency accuracy compared to Euler methods, at the cost of higher implementation complexity.
$$ (4) \quad s = \frac{2}{T_s}\frac{z-1}{z+1} $$

Where $T_s$ is the discrete time interval.

Now, discretization methods being a broad topic and out of the scope of this article, the following section will focus on the forward Euler method. But a similar approach can be used for the other two aforementioned methods.

To discretize a continuous-time system, we approximate derivatives using the Forward Euler method. The continuous time fonction: $\frac{dx(t)}{dt}$ is then approximated with the forward difference:

$$ \frac{dx(t)}{dt} ≈ \frac{x[n+1] – x[n]}{T_s} $$

This estimates the rate of change using the next time step (hence the forward difference).

Taking the Z-transform of the above leads to:

$$Z\{\frac{x[n+1] – x[n]}{T_s}\}= \frac{zX(z) – X(z)}{T_s} = \frac{z-1}{T_s}X(z) $$

This results in mapping the continuous time derivation function $\frac{d}{dt}$ to $\frac{z-1}{T_s}$ in the z-domain.

In the Laplace domain, differentiation corresponds to multiplication by $s$. Using the forward Euler approximation, we substitute:

$$ s ≈ \frac{z-1}{T_s} $$

This allows us to translate a continuous-time model into a discrete-time one by replacing $s$ with $s ≈ \frac{z-1}{T_s} $

The discretized equation of the PI controller using the forward Euler method would then result in the following equation:

$$ (5) \quad C(z) = \frac{Y(z)}{E(z)} = K_p + K_i T_s \frac{1}{z-1} $$

In the end, as the objective is to implement a PI controller inside of a digital control system, the discretized PI controller can then be translated into the following difference equations for run-time code generation:

$$ (6) \quad \begin{aligned}
& y(k) = P(k) + I(k) = k_p \cdot e(k) + I(k)\\
& I(k) = I(k-1) + k_i \cdot T_s \cdot e(k-1) \\
\end{aligned}$$

Where $e(k)$ is the error input (the difference between the targeted setpoint and the measured value) and $y(k)$ is the output of the PI controller.

PI controller tuning strategies

Many different strategies can be used for the tuning of PI controllers, such as Ziegler Nichols, loop shaping, optimization, pole placement, etc. Tuning should consider tradeoffs between tracking performance, load perturbance rejection, effect of measurement noise and other aspects, depending on the control requirements [2].

This section will further detail a popular optimization method, the magnitude optimum, often chosen for its good tradeoff between simplicity and performance. This tuning strategy will aim for a good response to setpoint changes, with the potential drawback of poor perturbance rejection. Alternatively, the symmetric optimum criterion can be used when the focus towards disturbance rejection [5].

The Magnitude (or Modulus) optimum tuning method’s objective is to design a controller so that the overall system’s output (controller + plant) would exactly and instantaneously reproduce its input. That is, the overall system’s transfer function would be unity [6].

To derive the magnitude optimum’s parameters, a first order plant model is considered, described in the Laplace domain, by equation below:

$$ (7) \quad P_1(s) = \frac{K_1}{1+s T_1}$$

The PI controller transfer function is rewritten as:

$$ (8) \quad C(s) = \frac{1+sT_n}{sT_i}$$

The actuator delay is also taken into account and approximated by a first order model as well:

$$ (9) \quad D(s) = e^{(-sT_{d,tot})} \approx \frac{1}{1+s T_{d,tot}}$$

We then obtain the open loop transfer function for the whole system (PI controller, actuator delay, plant):

$$H_{OL}(s) = C(s)D(s)P_1(s) = \frac{1+sT_n}{sT_i} \frac{1}{1+s T_{d,tot}} \frac{K_1}{1+s T_1}$$

Choosing the controller parameter $T_n = T_1$ to eliminate the dominant time constant pole at $s = -1/T_1$, we can simplify the open loop transfer function to:

$$H_{OL}(s) = \frac{K_1}{sT_i(1+sT_{d,tot})}$$

Computing the closed loop transfer function yields:

$$H_{CL}(s) = \frac{1}{1+s\frac{T_i}{K_1}+s^2\frac{T_iT_{d,tot}}{K_1}}$$

To compute the closed loop transfer function frequency gain, we can substitute $s$ by $jw$ and take the magnitude of the denominator:

$$den|H_{CL}(jw)|^2 = w^4(\frac{T_iT_{d,tot}}{K_1})^2 + w^2((\frac{T_i}{K_1})^2-2\frac{T_iT_{d,tot}}{K_1}) + 1$$

The low-frequency term (multiplier of $w^2$) is set to 0 to get the remaining control parameter $T_i$

$$(\frac{T_i}{K_1})^2-2\frac{T_iT_{d,tot}}{K_1} = 0 \implies T_i = 2K_1T_{d,tot}$$

This choice of $T_i$ aims to keep the closed loop transfer function close to one for lower frequencies.

The obtained generic formulas for magnitude optimum, shown below, can then be used for tuning PI controllers [5].

$$ (10) \quad \begin{aligned}
&T_n = T_1\\
&T_i = 2 K_1 T_{d,tot}
\end{aligned}$$

For the symmetric optimum, the generic formulas are shown below [5]

$$ (11) \quad \begin{aligned}
&T_n = 4 T_{d,tot}\\
&T_i = 8 K_1 T_{d,tot}^2
\end{aligned}$$

Rewriting (8) as in (1) results in the following equations for $K_p$ and $K_i$:

$$ (12) \quad \begin{aligned}
&K_p = T_n /T_i\\
&K_i = 1 / T_i
\end{aligned}$$

The parameter $T_{d,tot}$ represents the sum of all the delays in the system (from the data acquisition to the control output). For a practical example of PI controller tuning, please refer to: PI based current control.

PI controller configuration

Several techniques are available to improve the behavior of PI controllers. For instance, anti-windup strategies, setpoint weighting, feedforward, cascaded control are some of the improvements that can be made to conventional PI controllers [1]. A strategy to limit integrator windup is given in the section below.

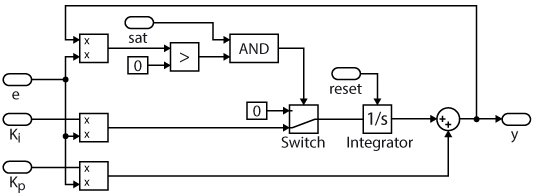
Integrator wind-up and anti-windup methods

When the control system has to adjust for a large disturbance or setpoint variation, the integrator will accumulate a significant error (wind-up) during the transient phase. This can also happen when a physical variable reaches its limits (in the case of a switched-mode power supply, the duty cycle is usually bounded between 0 and 1 for instance). So when the output finally reaches the reference, the large value accumulated by the integral term will create a significant, undesired overshoot of the output.

To get rid of this unwanted effect, anti-windup algorithms can be implemented. Several techniques are commonly used such as [1]:

Conditional integration
Back calculation
Automatic reset

The below illustration details the conditional integration algorithm, which will disable the integrator when the two following conditions are fulfilled:

The PI controller output saturates.
The control and error signals have the same sign (When they don’t, the integrator can help push the controller’s output out of saturation).

Conditional integration anti-windup algorithm for PI controllers — Conditional integration anti-windup algorithm

Reset

While the control task is not actively running (during system initialization, shutdown, or when transitioning between control modes for instance) it is often necessary to prevent the integrator from accumulating error. PI controllers commonly provide an external reset mechanism to address this. As part of the imperix blockset, the Core state block outputs the appropriate reset signal which can directly be connected to the external reset input of PI controllers. Obviously, this signal is only relevant in an experimental setup and is of no use in simulation.

B-Box / B-Board implementation

Simulink and PLECS

The (discrete) PID controller blocks from Simulink and PLECS can generally be used for the implementation of control algorithms. Please refer to the page Current control with a PI controller for configuration examples of both Simulink and PLECS PI controllers.

C/C++ code

The imperix IDE provides numerous pre-written and pre-optimized functions. Controllers such as P, PI, PID and PR are already available and can be found in the controllers.h/.cpp files.

As for all controllers, PI controllers are based on:

A pseudo-object PIDcontroller, which contains pre-computed parameters as well as state variables.
A configuration function, meant to be called during UserInit(), named ConfigPIDController().
A run-time function meant to be called during the user-level ISR such as UserInterrupt(), named RunPIController().

Note that this C/C++ implementation of the PI controller is slightly different from the one described above. More information on this implementation can be found in [5].

Imperix CPP IDE — Project view in imperix CPP IDE

References

[1] A. Visioli, “Practical PID Control”, 2006
[2] Karl J. Åström and Tore Hägglund, “Advanced PID Control”, 1995
[3] Buso, S. and Mattavelli, P., “Digital Control in Power Electronics: Second Edition”, 2015
[4] Franklin, G.F., Powell, J. and D.Workman, M.L., “Digital Control of Dynamic Systems”, 1998
[5] J. W. Umland and M. Safiuddin, “Magnitude and symmetric optimum criterion for the design of linear control systems: what is it and how does it compare with the others?,” in IEEE Trans. on Industry Applications, May-June 1990.
[6] Longchamp, R., “Commande numérique de systèmes dynamiques: cours d’automatique”, 2010