Alpha-Beta-Zero to dq0

The “Alpha-Beta-Zero to dq0” block converts a space vector from a stationary (αβ0) to a rotating reference frame (dq0). The angle of the rotating reference frame is given by the second input \(\theta=\omega t\).

The transformation is performed using the following rotation:

$$ \begin{bmatrix} V_d\\V_q\\V_0\end{bmatrix}
=\begin{bmatrix} \cos\theta & \sin\theta & 0 \\ -\sin\theta & \cos\theta & 0 \\ 0 & 0 & 1\end{bmatrix}\cdot
\begin{bmatrix} V_\alpha\\V_\beta\\V_0\end{bmatrix}$$

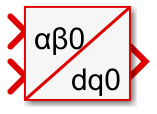
Simulink block

Signal specification

Parameters

None.

PLECS block

None. The PLECS block Transformation SRF->RRF can be used instead.

C++ functions

The user template located in the installation folder of CPP SDK contains an API folder with implementations of the coordinate transformation functions. The αβ0 to dq0 function is the following:

void ABG2DQ0(SpaceVector *rotating, const SpaceVector *fixed, const float theta);
Code language: C++ (cpp)

Parameters

• rotating: pointer on the dq0 space vector that will be updated. The SpaceVector structure is defined below.
• fixed: pointer on the αβ0 space vector that will be transformed. The SpaceVector structure is defined below.
• theta: the angle of the rotating reference frame, in radians.

typedef struct{
	float real;       // d- or alpha-axis component
	float imaginary;  // q- or neta-axis component
	float offset;     // homopolar component
} SpaceVector;Code language: C++ (cpp)