Table of Contents
What is the difference between Space Vector (SVPWM) and Sinusoidal Pulse Width Modulation (SPWM)? This article presents the advantages of the SVPWM technique over SPWM in the case of a two-level three-phase inverter.
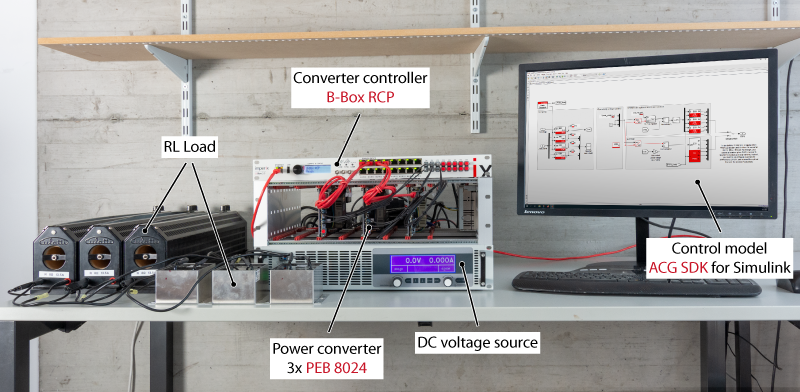
A demonstration code example is provided and freely available. It can be tested in simulation using imperix ACG SDK and validated in the laboratory with a B-Box RCP programmable controller and PEB half-bridge power modules.

What are SVPWM and SPWM?
SVPWM and SPWM are two modulation techniques commonly used with power converters. The purpose of a modulation scheme is to translate a voltage reference into a sequence of switching signals, in order to produce that reference at the output of the converter. While both techniques share similar acronyms, they have fairly different approaches.
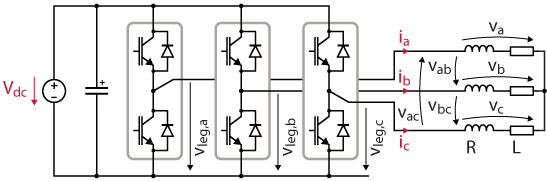
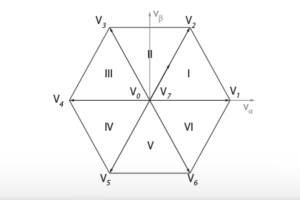
On one hand, the SVPWM technique represents each switching state of the converter by a space vector in the Clarke referential. Then, the desired output voltage is synthesized on average, by alternating between multiple space vectors over each switching period. On the other hand, SPWM is a Carrier-Based PWM scheme (CB-PWM) with a sinusoidal reference (see the note on the voltage source inverter). In order to simplify the comparison, only the case of two-level three-phase inverters is covered. The topology of the inverter is shown in the figure below.
Limitation of the DC bus utilization with SPWM
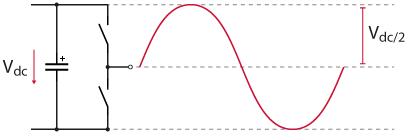
While producing a sinusoidal phase voltage with a two-level inverter, the peak amplitude is limited by the DC bus voltage [1]. Based on the illustration below, each leg of the inverter can produce a leg voltage \(v_{leg}\) of amplitude \(V_{DC}/2\).
The relative amplitude of the output voltage is often referred to as the modulation index, denoted \(m\) [1], and the maximum amplitude of the sinusoidal voltage corresponds to \(m = 1\). Thus, the phase voltage can be expressed as a function of the modulation index \(m\), the angular frequency \(\omega\), and the phase \(\phi\):
$$v_{phase}(t) = m \, \frac{V_{DC}}{2} \, \sin(\omega \, t + \phi)$$
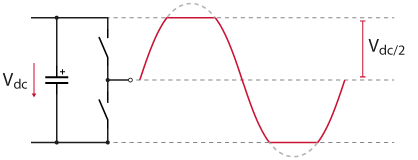
If \(m > 1\), the output voltage will be clipped to \(\pm V_{DC}/2\). As such, the distortion introduces low-order harmonics that can be difficult to filter out. If the voltage reference exceeds the DC bus capabilities, the converter is said to be in the overmodulation region.
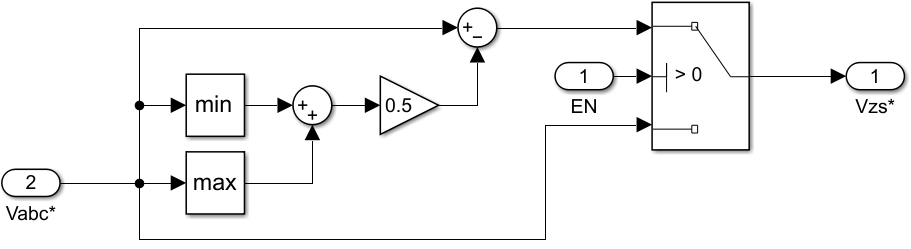
Min/max injection with SVPWM
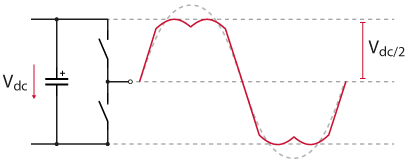
It can be demonstrated that SVPWM is equivalent to an SPWM with min/max injection [1]. The idea behind the min/max injection method is to add a triangular zero sequence component (triplen harmonics) to the sinusoidal reference, which distorts the phase voltage references. This way, the peak voltage of the reference is reduced in comparison to a pure sinusoidal reference, and the modulation index can be increased up to \(m = 2 / \sqrt{3} \approx 1.15\) before hitting the limits of the DC bus voltage.
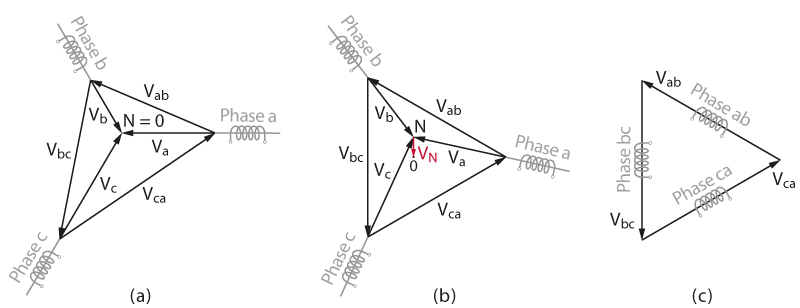
If the inverter is connected to a load with a grounded star connection, the distortion of the phase voltages is propagated to the line-to-line voltages, as shown below in Fig. (a). As a result, the load currents are also distorted, and SVPWM is not a suitable modulation scheme in terms of harmonic content. Fortunately, it is possible to suppress the distortions in the line-to-line voltages by using different wiring of the load. If the star connection is floating – see Fig. (b) – the triplen harmonics of the zero-sequence will cancel each other out, and the line-to-line voltages remain unaffected. The situation is similar in the case of a delta-connected load – see Fig. (c) – since the phase voltages of the load are equal to the line-to-line voltages produced by the inverter. Thus, for delta or floating star connections, SVPWM allows increasing the maximum line-to-line voltage without distortion of the load currents.
Experimental comparison
Simulink implementation
The model provided in this article executes a simple open-loop voltage control of a two-level three-phase inverter. For comparison purposes, both SVPWM and SPWM (with or without min/max injection) techniques are implemented in parallel, and the user can select which switching signals will drive the converter.
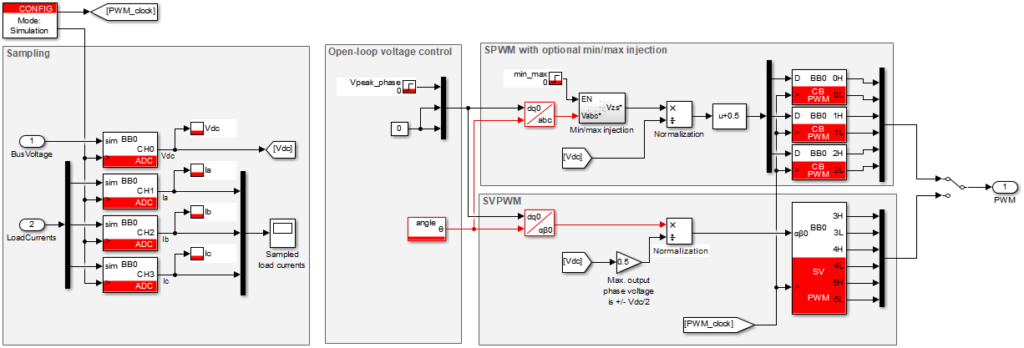
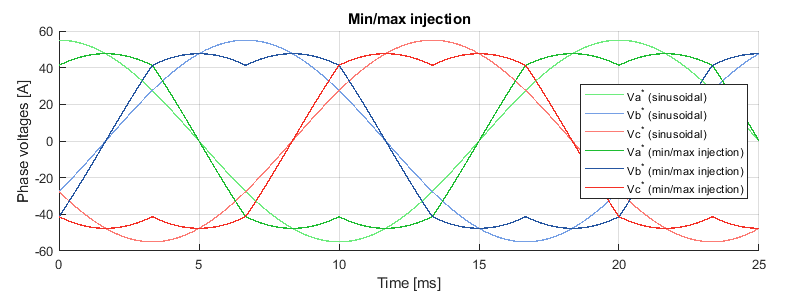
The implementation of SVPWM with Simulink and the ACG SDK can be found in the space vector modulation (SVM) note. Similarly, the details on the SPWM implementation can be found in the three-phase inverter note. Finally, the min/max injection for a carrier-based PWM is illustrated in the figure below.
SVPWM and SPWM waveforms
During the experiments, the two-level converter was connected to a balanced three-phase RL load, under the following conditions:
- DC bus voltage: 100 V
- Control frequency and sampling: 20 kHz
- Sampling phase: 0.5
- Load resistance: 8.5 Ω
- Load inductance: 2.5 mH
The experimental setup is presented in the picture below. The power converter is built from 3x PEB 8024 phase-leg modules and is controlled by a B-Box RCP prototyping controller. The control software is implemented graphically using the ACG SDK library for Simulink.
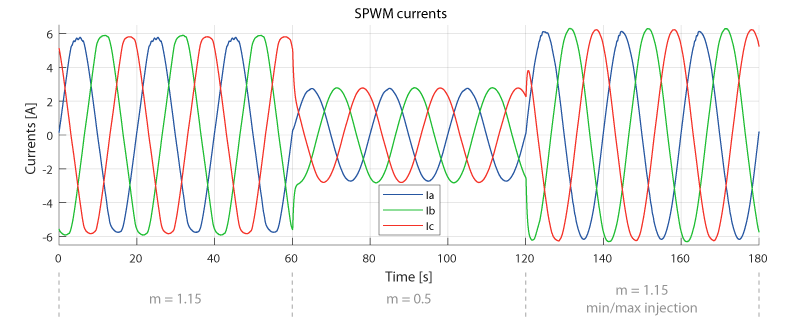
The goal is to observe whether the line-to-line voltages are distorted or not, depending on the modulation scheme in use. Since the output line-to-line voltages of the converter are switched, it would require heavy filtering to extract sinusoidal waveforms. Instead, the line-to-line voltages can be observed indirectly through the load currents, since they are filtered by inductors. Then, in order to evaluate the impact of the modulation scheme, the modulation index is toggled between \(m = 0.5\) and \(m = 1.15\) each 60 ms.
When the modulation index is \(m = 1.15\), the SPWM technique is in its overmodulation region. As a result, the output currents are flattened at their maximum, as shown in the figure below between \(t = 0\, ms\) and \(t = 60\, ms\). However, the currents are undistorted if the SPWM is used in combination with a min/max injection, as observed after \(t = 120\, ms\).
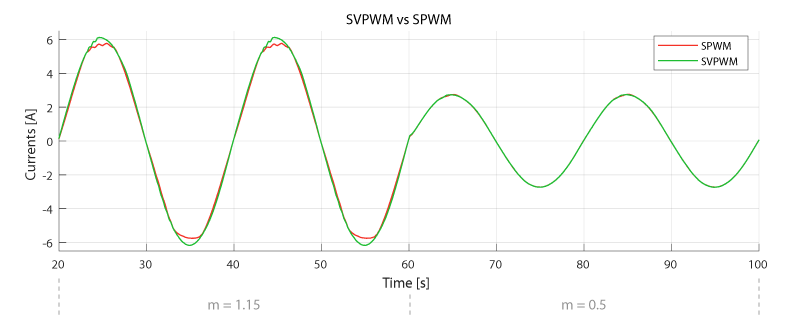
The absence of distortion at \(m = 1.15\) with min/max injection – or SVPWM, since the methods are equivalent – is easier to observe by superimposing the experimental currents obtained with SPWM and SVPWM, as shown below. For \(m = 0.5\) though, the output voltages are within the capabilities of the DC bus with both modulation techniques, and the currents are identical regardless of the zero-sequence injection.
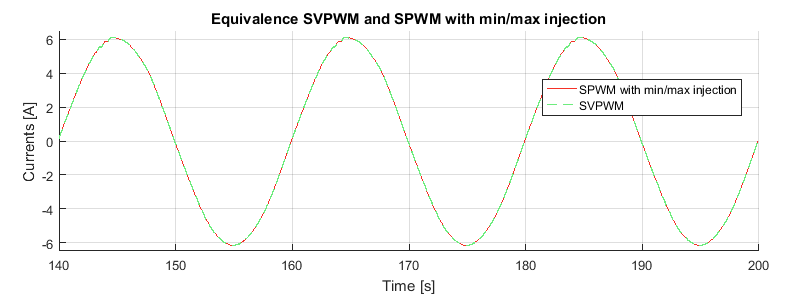
The equivalence between SVPWM and SPWM with min/max injection was also verified experimentally, by using both methods with \(m = 1.15\) and superimposing the measured currents, as shown below.
While the voltage waveforms are challenging to measure experimentally (switched waveforms), their references can be observed directly from the control. The figure below illustrates side-by-side the sinusoidal voltage references and the corresponding min/max zero-sequence, with its characteristic triangular shape [1].
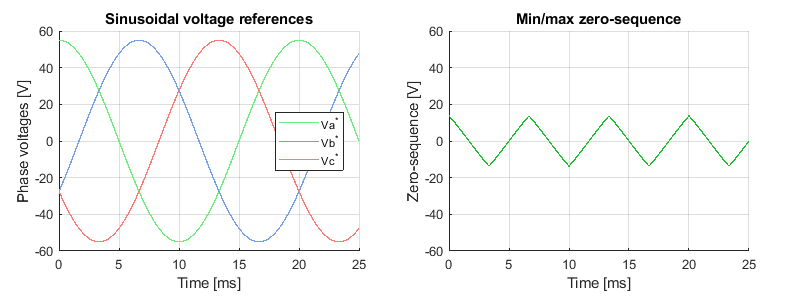
By subtracting the zero-sequence from the sinusoidal waveforms, one can obtain the saddle-shaped voltage references from SVPWM.
Academic references
[1] Slobodan N. Vukosavic, “Grid-Side Converters Control and Design”, Springer, 2018, ISBN: 978-3-030-10346-0