Fixed point vs floating point arithmetic in FPGA

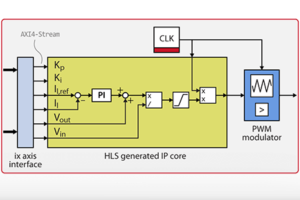
The choice of fixed vs floating-point arithmetic for an FPGA algorithm is a decision that has a significant impact on the FPGA resources usage, computation latency, as well as data precision. This page provides a comparison between fixed-point vs floating-point arithmetic and gives advantages and drawbacks for each approach. Then, it shows how to use the typecast MATLAB function in MATLAB Simulink to transform a floating-point value into an integer without changing the underlying bits, which is useful when exchanging data between the CPU and FPGA of an imperix power converter controller.

Integers and fixed-point arithmetic in FPGA

A fixed-point number is represented with a fixed number of digits before and after the radix point. In FPGA, a fixed-point number is stored as an integer that is scaled by a specific implicit factor. For example, the common notation fix16_10  used by Xilinx stands for a 16-bit integer scaled by \(2^{10}\). In other words, 10 out of the 16 bits are used to represent the fractional part and 6 bits for the integer part.

Fixed-point arithmetic is widely used in FPGA-based algorithms because it usually runs faster and uses fewer resources when compared to floating-point arithmetic.

However, one drawback of fixed-point arithmetic is that the user has to anticipate the range of the data and choose the scaling factor accordingly (the size of the fractional part), making the design more prone to errors.

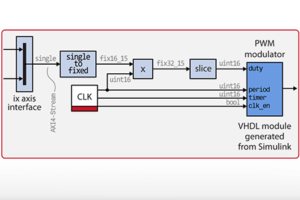
The custom FPGA PWM modulator is a good example where it makes sense to use fixed-point arithmetic, given that the range of the duty-cycle parameter is restricted between 0.0 and 1.0.

Floating-point arithmetic in FPGA

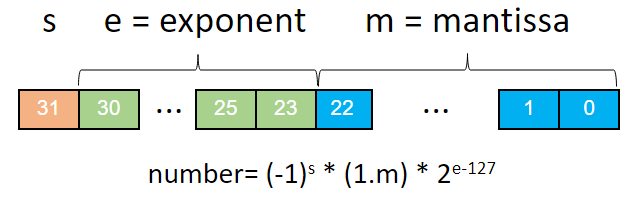
A floating-point number is represented with a fixed number of significant digits and scaled using an exponent in some fixed base. There are three formats supported by Xilinx tools: half (16 bit), single (32 bit), and double (64 bit). For example, a single format number is represented as:

Floating-point-based algorithms are more complex to handle than fixed-point, especially when using HDL languages (VHDL, Verilog). Fortunately, various Xilinx tools (such as the Vivado Floating-Point IP and other High-Level Synthesis (HLS) tools) make the development of floating-point-based algorithms much more convenient. Indeed, these tools add an abstraction level so that the user does not need to handle data representations to their binary representation level.

We recommend starting a design by using the single format everywhere and then switching to fixed-point arithmetic, where necessary, to improve latency and resource utilization.

How to typecast in MATLAB Simulink

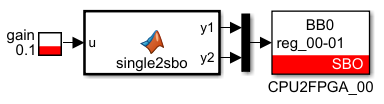
To typecast a floating point to an integer in MATLAB Simulink, the following MATLAB Function can be used. It uses the typecast instruction to alter the type of a variable without modifying the underlying binary number. As FPGA registers are 16-bits, this transformation is required in order to transform a 32-bit floating-point value into two 16-bit registers and transfer it from the CPU to the FPGA using.

function [y1,y2] = single2sbo(u)
  temp = typecast(single(u),'uint16');
  y1 = temp(1);
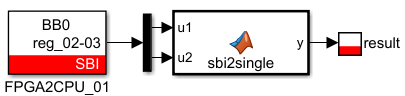
  y2 = temp(2);Code language: Matlab (matlab)

Typecasting an integer to a floating point in MATLAB Simulink is the reverse operation. It consists of concatenating two uint16 values and interpreting the result as single-precision data using the typecast MATLAB function.

function y = sbi2single(u1,u2)
  y = single(0); % sets compiled size of output
  y = typecast([uint16(u1) uint16(u2)], 'single');Code language: Matlab (matlab)

A use-case example of the MATLAB typecast function can be seen in the High-Level Synthesis for FPGA developments example.