Knowledge base » Technical notes » FPGA implementation of a PLL for grid synchronization

FPGA implementation of a PLL for grid synchronization

Shu Wang June 23, 2021April 8, 2024 Updated onApril 8, 2024 TN143

Table of Contents

The operation of a grid-tied power converter (such as the 3-phases PV inverter) requires that the control software implements a grid synchronization technique. One well-known approach consists in using a three-phase PLL to project the AC grid quantities into a synchronous rotating reference frame. The PLL algorithm is usually executed on the CPU of the controller, but it can be alternatively offloaded to the FPGA.

Besides the obvious benefit of offloading the CPU, the execution of the synchronization algorithm on an FPGA also allows for a much shorter control latency, ultimately enabling full-FPGA ultra-fast control loops, as presented in FPGA-based inverter control.

This note will cover the implementation of a simple PLL-based grid synchronization algorithm that is suitable for being executed on the FPGA of the B-Box and B-Board controllers.

Overview of the grid synchronization module

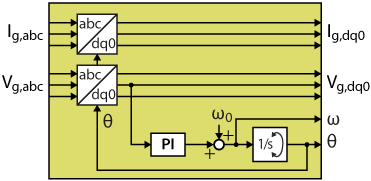
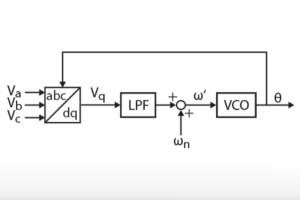
The grid synchronization algorithm implemented in FPGA is based on a conventional DQ-PLL, similar to the CPU implementation presented in the TN103. The PLL consists of an abc-to-dq transformation (used as a phase detector), a PI regulator (used as a low-pass filter), and a wrapping integrator (used as a voltage-controlled oscillator). The grid synchronization module also projects the measured grid current into the synchronously rotating reference frame, so the projected dq components can be used by the FPGA-based dq current control module.

Schematic of the FPGA-based grid synchronization module with DQ-PLL

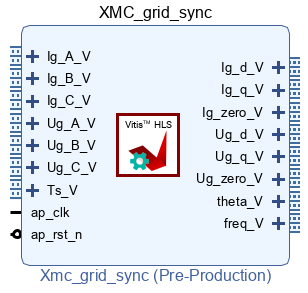
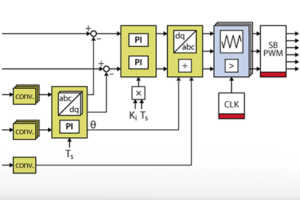
The following sections detail how to pack that algorithm into the FPGA IP shown below, using both High-Level Synthesis tools Vitis HLS and Model Composer. That IP uses AXI4-Stream inputs and outputs to be compatible with other IPs developed on other pages, as well as with Xilinx IP cores for Vivado.

Generated IP of the grid synchronization module

Further details on integrating that IP into the FPGA are presented on the High-Level Synthesis page. A complete converter control algorithm that uses that IP is presented in FPGA-based converter control.

To find all FPGA-related notes, you can visit FPGA development homepage.

FPGA implementation of the PLL with Model Composer (Simulink)

The sources of the grid synchronization module developed with Xilinx Model Composer can be downloaded below. To generate a Vivado IP from this model using Model Composer’s automatic code generation please refer to the introduction to Model Composer.

Download TN143_FPGA_Grid_Sync_Model_Composer.zip

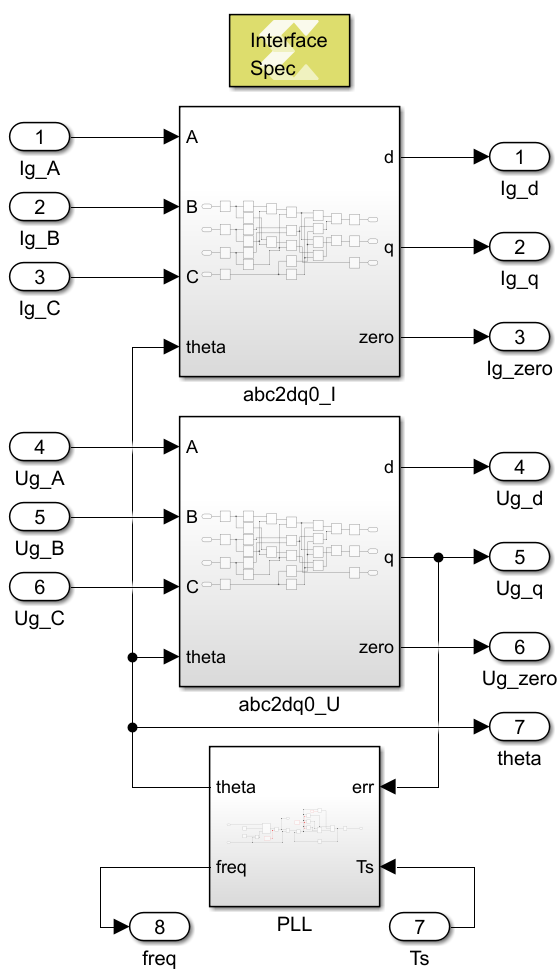
Grid synchronization module implemented with Model Composer — Top-level of the grid synchronization module

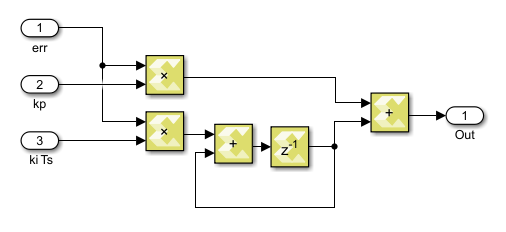
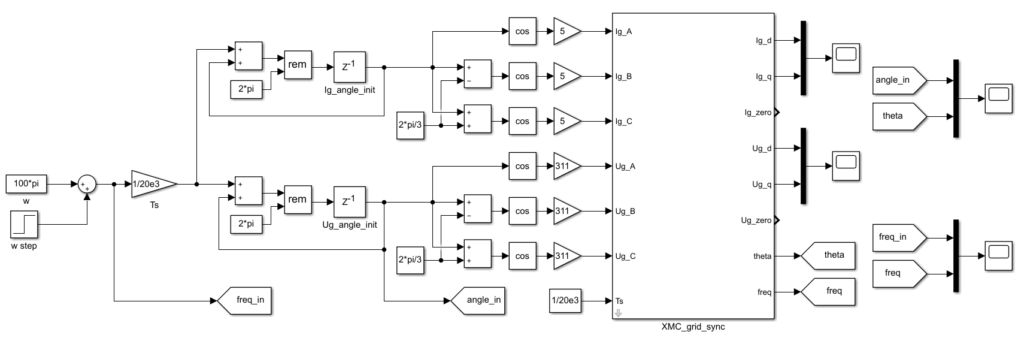
Basically, this module includes two abc-to-dq0 transformations and one PLL. The PI controller used within the PLL block is based on the implementation presented in the Model Composer introduction.

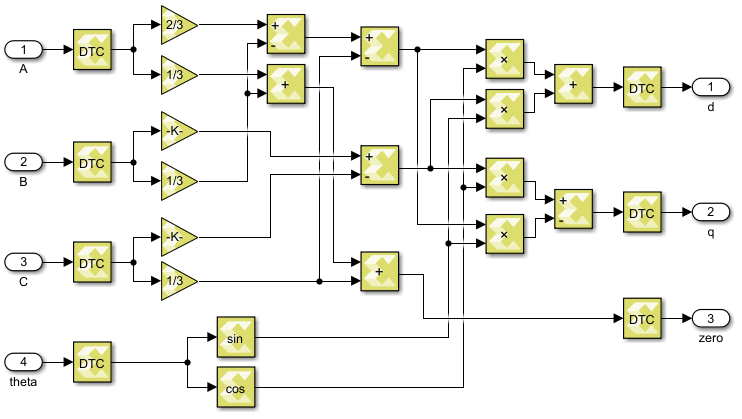
The abc-to-dq0 transformation simply implements the mathematical formulae introduced in abc to dq0. In both Vitis HLS and Model Composer, fixed-point types are used to represent the intermediary results. Specifically, all the angles (radians) are represented with fix16_12 and the other quantities are represented with fix32_16. The main reason is that floating-point trigonometric functions are computationally heavy and cannot meet the timing requirement. As a side benefit, using fixed-point operations also improves the resource usage and latency of the other operations (multiplications and additions). Nevertheless, to ensure compatibility with other modules, the inputs and outputs of the coordinate transformations are converted into floating-point types.

As seen later in the section “Precision of the fixed-point approach”, the loss of precision caused by the use of fix16_12 numbers for representing angles is negligible in practice (lost in the noise), although small differences can be seen in simulation.

abc-to-dq0 transformation implementation with Xilinx Model Composer — abc-to-dq0 transformation implementation with Model Composer

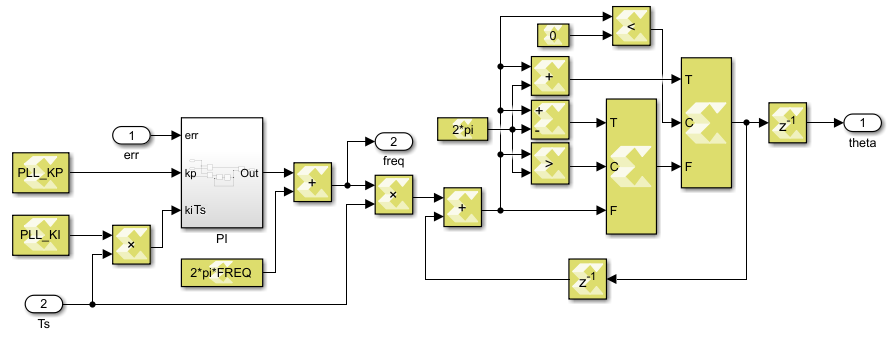
DQ-PLL implementation with Xilinx Model Composer — PLL implementation with Model Composer

PI controller implementation with Xilinx Model Composer — PI controller implementation with Model Composer

The fixed-point trigonometric functions in Vitis HLS (math library) are calculated using the CORDIC algorithm. For those interested, open “hls_math.h” to see how math functions are implemented in HLS, or look at Vitis HLS math library for reference.
In Model Composer, there is no need to specify the data types or implementation methods, and the software will automatically call the HLS math library during code generation.

Testbench of the Model Composer implementation

One main advantage of Model Composer over Vitis HLS is that test benches can be easily run directly from within Simulink. The testbench generates 50 Hz three-phase voltages and currents and passes them as inputs to the developed PLL. To test the frequency tracking of the PLL, the input frequency is stepped to 52 Hz at t=0.02s.

Mathematically, the inputs of the testbench are:

Voltages	Currents	Time
$$\begin{aligned} &U_{a}=311\cdot\sin(2\pi f nT_{s}) \\ &U_{b}=311\cdot\sin(2\pi f nT_{s} – 2\pi/3) \\ &U_{c}=311\cdot\sin(2\pi f nT_{s} + 2\pi/3)\end{aligned}$$	$$\begin{aligned}&I_{a}=5\cdot\sin(2\pi f nT_{s}) \\ &I_{b}=5\cdot\sin(2\pi f nT_{s} – 2\pi/3) \\ &I_{c}=5\cdot\sin(2\pi f nT_{s} + 2\pi/3) \end{aligned}$$	$$\begin{aligned}&n=0,1,2,…,1999 \\ &T_s=50\,\text{µs} \\ &f=\begin{cases}50 & n\leqslant 400 \\ 55 & n>400 \end{cases} \end{aligned} $$

Testbench of the grid synchronization module developed with Xilinx Model Composer — Testbench of the PLL developed with Xilinx Model Composer

After running the Simulink-based simulation, the inputs and outputs can be exported to the MATLAB workspace and plotted, as shown below.

Testbench results of the Model Composer implementation

The simulation results are identical to the Vitis HLS approach shown below.

FPGA implementation of the PLL with Vitis HLS (C++)

The full Vitis HLS implementation of the PLL can be downloaded below and the main lines of code are given for reference.

Download TN143_FPGA_Grid_Sync_Vitis_HLS.zip

#include "grid_sync.h"

#include <hls_stream.h>
#include <stdint.h>
#include "ap_fixed.h"
#include "hls_math.h"

void abc2dq0(float A, float B, float C, float wt, float& d, float& q, float& zero)
{
  #pragma HLS inline

  const ap_fixed<16,2> sqrt3_3 = 0.57733154296875;

  ap_fixed<32,16> A_fix = (ap_fixed<32,16>)A;
  ap_fixed<32,16> B_fix = (ap_fixed<32,16>)B;
  ap_fixed<32,16> C_fix = (ap_fixed<32,16>)C;
  ap_fixed<16,4> wt_fix = (ap_fixed<16,4>)wt;

  ap_fixed<32,16> beta_fix = (B_fix-C_fix)*sqrt3_3;
  ap_fixed<32,16> zero_fix = (A_fix+B_fix+C_fix)/3;
  ap_fixed<32,16> alpha_fix = A_fix-zero_fix;

  ap_fixed<16, 2> cos_wt = hls::cos(wt_fix);
  ap_fixed<16, 2> sin_wt = hls::sin(wt_fix);

  ap_fixed<32,16> d_fix = alpha_fix*cos_wt + beta_fix*sin_wt;
  ap_fixed<32,16> q_fix = -alpha_fix*sin_wt + beta_fix*cos_wt;

  d = (float)d_fix;
  q = (float)q_fix;
  zero = (float)zero_fix;
}

void pll(float Ugq, float Ts, float& theta, float& freq)
{
  #pragma HLS inline

  const float theta_max = 6.283185307179586;
  const float theta_min = 0;

  static float pll_accum = 0;
  #pragma HLS RESET variable=pll_accum

  float pll_kiTs = pll_ki*Ts;
  pll_accum += pll_kiTs* Ugq;
  float pi_out = pll_kp * Ugq + pll_accum;
  float w = pi_out + w0;

  static float wrapping_accum = 0;
  #pragma HLS RESET variable=wrapping_accum

  wrapping_accum += Ts * w;

  if(wrapping_accum > theta_max) {
    wrapping_accum -= theta_max;
  } else if(wrapping_accum < theta_min) {
    wrapping_accum += theta_max;
  }

  theta = wrapping_accum;
  freq = w;
}

void vitis_grid_sync(	hls::stream<float>& in_Iga,
hls::stream<float>& in_Igb,
hvoid vitis_grid_sync(
  hls::stream<float>& in_Iga,
  hls::stream<float>& in_Igb,
  hls::stream<float>& in_Igc,
  hls::stream<float>& in_Uga,
  hls::stream<float>& in_Ugb,
  hls::stream<float>& in_Ugc,
  hls::stream<float>& in_Ts,
  hls::stream<float>& out_Igd,
  hls::stream<float>& out_Igq,
  hls::stream<float>& out_Ig0,
  hls::stream<float>& out_Ugd,
  hls::stream<float>& out_Ugq,
  hls::stream<float>& out_Ug0,
  hls::stream<float>& out_theta,
  hls::stream<float>& out_freq)
{
  #pragma HLS INTERFACE axis port=in_Iga
  #pragma HLS INTERFACE axis port=in_Igb
  #pragma HLS INTERFACE axis port=in_Igc
  #pragma HLS INTERFACE axis port=in_Uga
  #pragma HLS INTERFACE axis port=in_Ugb
  #pragma HLS INTERFACE axis port=in_Ugc
  #pragma HLS INTERFACE axis port=in_Ts
  #pragma HLS INTERFACE axis port=out_Igd
  #pragma HLS INTERFACE axis port=out_Igq
  #pragma HLS INTERFACE axis port=out_Ig0
  #pragma HLS INTERFACE axis port=out_Ugd
  #pragma HLS INTERFACE axis port=out_Ugq
  #pragma HLS INTERFACE axis port=out_Ug0
  #pragma HLS INTERFACE axis port=out_theta
  #pragma HLS INTERFACE axis port=out_freq
  #pragma HLS INTERFACE ap_ctrl_none port=return

  float Iga = in_Iga.read();
  float Igb = in_Igb.read();
  float Igc = in_Igc.read();
  float Uga = in_Uga.read();
  float Ugb = in_Ugb.read();
  float Ugc = in_Ugc.read();
  float Ts = in_Ts.read();

  float Igd,Igq,Ig0,Ugd,Ugq,Ug0,w;
  static float wt;
  #pragma HLS RESET variable=wt

  abc2dq0(Uga, Ugb, Ugc, wt, Ugd, Ugq, Ug0);
  abc2dq0(Iga, Igb, Igc, wt, Igd, Igq, Ig0);
  pll(Ugq, Ts, wt, w);

  out_Igd.write(Igd);
  out_Igq.write(Igq);
  out_Ig0.write(Ig0);
  out_Ugd.write(Ugd);
  out_Ugq.write(Ugq);
  out_Ug0.write(Ug0);
  out_theta.write(wt);
  out_freq.write(w);
}
Code language: C++ (cpp)

The code is divided into the following functions:

void abc2dq0(float A, float B, float C, float wt, float& d, float& q, float& zero)
Transforms the three-phase AC quantities A, B, C into d, q, zero components, using the reference frame angle wt.
void pll(float Ugq, float Ts, float& theta, float& freq)
Runs a discrete PI controller (with discretization period Ts) using the alignment error Ugq and updates the output angle (theta, in rad) and frequency (freq, in rad/s). The controller parameters pll_kp and pll_ki, as well as the central frequency w0, are defined in the grid_sync.h file.
void vitis_grid_sync( ... )
Runs the PLL algorithm on the grid quantities in_Igabc and in_Ugabc to compute the grid angle (out_theta) and frequency (out_freq), as well as the components of the grid quantities in the dq synchronous reference frame.

The wrapping integrator is implemented using the code below, to avoid the modulo-based wrapping used in the CPU version. Since this approach only uses switches and comparators, it is much better suited to an FPGA implementation than the resource-consuming modulo function.

const float theta_max = 6.283185307179586;
const float theta_min = 0;

static float wrapping_accum = 0;
#pragma HLS RESET variable=wrapping_accum

wrapping_accum += Ts * w;

if(wrapping_accum > theta_max)
{
  wrapping_accum -= theta_max;
}
else if(wrapping_accum < theta_min)
{
  wrapping_accum += theta_max;
}Code language: C++ (cpp)

Note that the vitis_grid_sync method uses AXI4-Stream interfaces to be compatible with the other functions developed for the TN147. More information about Vitis HLS can be found in the introduction to Vitis HLS, notably on how to create an IP out of the provided code to run the algorithm on the FPGA of a B-Box or B-Board controller.

#pragma HLS inline is a directive that removes a function as a separate entity in the hierarchy and enables optimization with surrounding operations. It’s recommended to use this directive when defining a child function in Vitis HLS. Look at pragma HLS inline (xilinx.com) to see more details.

Testbench of the Vitis HLS implementation

To validate the Vitis HLS implementation, a testbench can be built using the code provided below.

#include "grid_sync.h"
#include "math.h"
#include <hls_stream.h>
#include <stdint.h>
#include <stdio.h>
#include <stdlib.h>

#define ITERATIONS 2000
#define two_pi 6.283185307f

int main()
{
	/* Test signals */
	hls::stream<float> tb_in_Iga;
	hls::stream<float> tb_in_Igb;
	hls::stream<float> tb_in_Igc;
	hls::stream<float> tb_in_Uga;
	hls::stream<float> tb_in_Ugb;
	hls::stream<float> tb_in_Ugc;
	hls::stream<float> tb_in_Ts;
	hls::stream<float> tb_out_Igd;
	hls::stream<float> tb_out_Igq;
	hls::stream<float> tb_out_Ig0;
	hls::stream<float> tb_out_Ugd;
	hls::stream<float> tb_out_Ugq;
	hls::stream<float> tb_out_Ug0;
	hls::stream<float> tb_out_theta;
	hls::stream<float> tb_out_freq;

	/* Test inputs*/
	float in_Iga;
	float in_Igb;
	float in_Igc;
	float in_Uga;
	float in_Ugb;
	float in_Ugc;
	float in_Ts = 0.00005;		// fs = 20kHz
	float Ug_angle = 0;		// change to non-zero to see how pll converges
	float Ig_angle = 0;
	float freq_in = two_pi*50;	// fgrid = 50Hz
	float wt = freq_in*in_Ts;

	/* Test outputs */
	float out_Igd;
	float out_Igq;
	float out_Ugd;
	float out_Ugq;
	float out_theta;
	float out_freq;

	/* Create csv file to store simulation data*/
	FILE *inputs, *outputs;
	inputs = fopen ("inputs.csv", "w+");
	outputs = fopen ("outputs.csv", "w+");
	fprintf(inputs, "%s", "Uga,Ugb,Ugc,Iga,Igb,Igc\n");
	fprintf(outputs, "%s", "Ugd,Ugq,Igd,Igq,theta,theta_in,freq,freq_in\n");

	/* Run model */
	for (int i = 0; i < ITERATIONS; i++)
	{
		in_Uga = 311*cos(Ug_angle);
		in_Ugb = 311*cos(Ug_angle-two_pi/3);
		in_Ugc = 311*cos(Ug_angle+two_pi/3);
		in_Iga = 5*cos(Ig_angle);
		in_Igb = 5*cos(Ig_angle-two_pi/3);
		in_Igc = 5*cos(Ig_angle+two_pi/3);

		tb_in_Uga.write(in_Uga);
		tb_in_Ugb.write(in_Ugb);
		tb_in_Ugc.write(in_Ugc);
		tb_in_Iga.write(in_Iga);
		tb_in_Igb.write(in_Igb);
		tb_in_Igc.write(in_Igc);
		tb_in_Ts.write(in_Ts);

		vitis_grid_sync(tb_in_Iga,tb_in_Igb,tb_in_Igc,tb_in_Uga,tb_in_Ugb,tb_in_Ugc,tb_in_Ts,tb_out_Igd,tb_out_Igq,tb_out_Ig0,tb_out_Ugd,tb_out_Ugq,tb_out_Ug0,tb_out_theta,tb_out_freq);

		out_Igd = tb_out_Igd.read();
		out_Igq = tb_out_Igq.read();
		out_Ugd = tb_out_Ugd.read();
		out_Ugq = tb_out_Ugq.read();
		out_theta = tb_out_theta.read();
		out_freq = tb_out_freq.read();

		fprintf(inputs,"%f,%f,%f,%f,%f,%f %s",in_Uga,in_Ugb,in_Ugc,in_Iga,in_Igb,in_Igc,"\n");
		fprintf(outputs,"%f,%f,%f,%f,%f,%f,%f,%f %s",out_Ugd,out_Ugq,out_Igd,out_Igq,out_theta,Ug_angle,out_freq,freq_in,"\n");

		if(i>400)freq_in = two_pi*55;	// freq step at 0.02s
		wt = freq_in*in_Ts;
		Ug_angle = remainder((Ug_angle+wt),two_pi);
		Ig_angle = remainder((Ig_angle+wt),two_pi);
	}

	fclose(inputs);
	fclose(outputs);

	printf("------ Test Passed ------\n");

	/* End */
	return 0;
}
Code language: C++ (cpp)

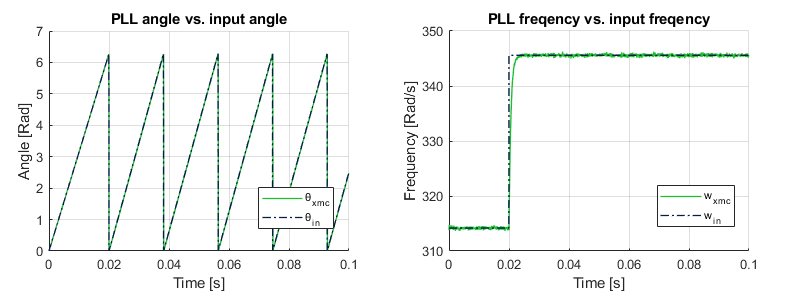
Here, the exact same testbench as with Model Composer (same inputs) is implemented. The C Simulation tool of Vitis HLS is used to run the testbench. The input and output data are stored in “Vitis_grid_sync\solution1\csim\build” and can be plotted for comparison (e.g. with MATLAB). The results are shown below:

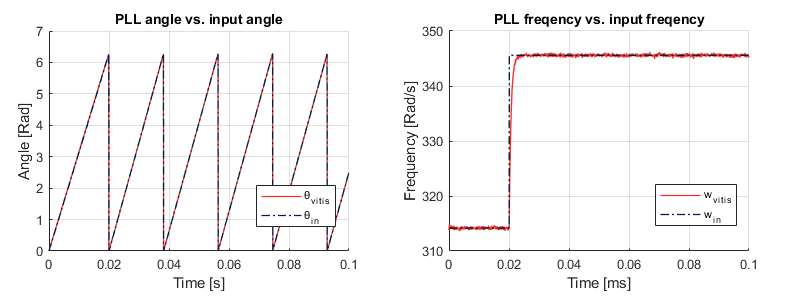
Simulation results of the grid synchronization module — Testbench results from C simulation of Vitis HLS model

The simulation results show that the angle and frequency estimated by the PLL follow the input accurately, although some noise with relatively low amplitude can be observed on the PLL frequency. This matter will be addressed in a dedicated section, and the performance will also be compared to the already validated CPU-based model provided with the imperix blockset.

Precision of the fixed-point approach

As introduced before, fix16_12 fixed-point angles are used inside the coordinate transformation blocks since floating-point trigonometric functions cannot meet the timing requirements. This conversion to fixed-point inevitably results in a loss of precision, which can be seen as “noise” in the testbench results.

For sake of validation, if the angle is represented with fix32_28 instead of fix16_12, all the visible estimation “noise” disappears completely, as illustrated below. Unfortunately, the implementation cannot meet the timing requirements if fix32_28 is used.

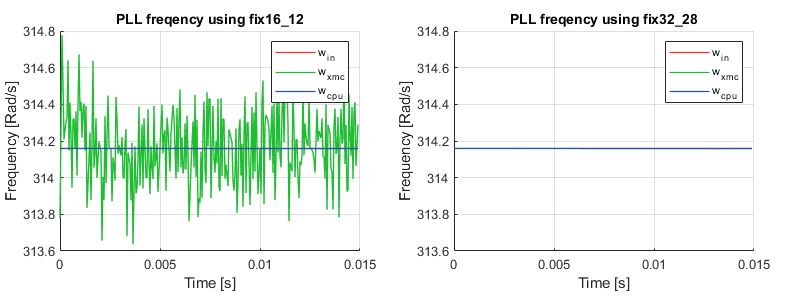
Comparison of resolution with fixed point FPGA implementation — Comparison of fixed-point representations with different resolutions used in Xilinx Model Composer (xmc).
A floating-point implementation (cpu) is also shown for reference.

Representing angles with fix16_12 numbers allows for an absolute angular resolution of $1/2^{12}\approx 0.00024 \,\text{rad}$, which corresponds to a precision of 0.004%. As for the other variables, using fix32_16 numbers gives an absolute resolution of $1/2^{12}\approx 15 \,\text{µV}$ or $\text{µA}$.

The simulation testbench results showed that the resulting error on the estimated frequency is at most 0.2%, which is considered acceptable in real systems, where the measurement accuracy is rather in the 1% range.

Usecase example

The developed FPGA PLL is used for grid synchronization in the FPGA ctrl of a grid-tied 3-phase inverter.

Shu Wang

Shu is an experienced development engineer at imperix. He authored or co-authored numerous articles on the knowledge base, notably on FPGA-based control implementation and high-level synthesis tools and techniques.

Technical notes

SOGI PLL

Antonin Stampbach and

Nicolas Cherix March 22, 2021July 5, 2024 TN104

Second-order Generalized Integrators (SOGI) have recently been proposed for use as phase detectors for PLL implementations. These structures are essentially notch filters (band-pass) that can be easily tuned to the grid frequency.

Technical notes

PI controller implementation for current control

Gabriel Fernandez March 23, 2021February 15, 2024 TN105

This note introduces the general operating principles of a simple Proportional-Integral PI controller. An example of current control for a boost converter is provided, along with a practical control implementation.

Technical notes

Vector current control

Gabriel Fernandez March 23, 2021February 15, 2024 TN106

Vector current control is a widespread current control technique for three-phase AC currents, which uses a rotating reference frame, synchronized with the grid voltage (dq-frame)

Technical notes

Cascaded voltage control

Gabriel Fernandez March 23, 2021May 15, 2024 TN108

This note introduces the general operating principles of cascaded control and then details a possible design methodology. Then, an example of cascaded voltage control for a boost converter is provided.

Technical notes

Proportional resonant controller

Antonin Stampbach and

Nicolas Cherix March 23, 2021May 16, 2024 TN110

A proportional resonant control can be seen as the implementation of PI controllers within a rotating reference frame (dq), which allows to re-locate the infinite DC gain at desired frequency.

Technical notes

Field oriented control (FOC) of permanent magnet synchronous machine (PMSM)

Simon Strobl March 23, 2021March 28, 2024 TN111

The Field-Oriented Control (FOC) method is a motor control strategy that orients the stator current vector in a rotating reference frame of the machine.

NEWSLETTER

CONTROL PRODUCTS

POWER PRODUCTS

COMPANY

Overview of the grid synchronization module

FPGA implementation of the PLL with Model Composer (Simulink)

Testbench of the Model Composer implementation

FPGA implementation of the PLL with Vitis HLS (C++)

Testbench of the Vitis HLS implementation

Precision of the fixed-point approach

Usecase example

Similar Posts

NEWSLETTER

CONTROL PRODUCTS

POWER PRODUCTS

COMPANY